Introduction
Integration is a core part of calculus, often presenting unique challenges that require creative ways to solve. In this post, I will share some of the interesting integration problems I have encountered, along with their solutions. Take some time to try them out before checking out my solutions!
Problem 1
Evaluate the integral within 30 seconds:
Solution:
$$ \begin{aligned} u &= x^{\frac{1}{\ln(x)}} \\ &= e^{\ln(x) \times \frac{1}{\ln(x)}} \\ &= e \\ \int e \, dx &= ex + C \end{aligned} $$Problem 2
Evaluate the integral:
Solution:
Let \(u = 1 + ln(x)\) and \( x = e^{u-1} \)
Then \(du = \frac{1}{x} dx\) then \( du = \frac{1}{e^{u-1}} \)
The limits change as follows:
- When \(x = 1\), \(u = 1 + \ln(1) = 1\)
- When \(x = e\), \(u = 1 + \ln(e) = 2\)
The integral becomes:
$$ \int_1^2 \frac{(u-1)}{u^2} \, e^{u-1} \, du \\ = \int_1^2 \frac{e^{u-1}}{u} \, du - \int_1^2 \frac{e^{u-1}}{u^2} \, du \\ $$Using integration by parts on the second integral and by differentiating \(e^{u-1}\):
$$ \int_1^2 \frac{e^{u-1}}{u^2} \, du = - \frac{e^{u-1}}{u} \bigg|_1^2 + \int_1^2 \frac{e^{u-1}}{u} \, du $$Substituting back, we have:
$$ \int_1^2 \frac{e^{u-1}}{u} \, du + \frac{e^{u-1}}{u} \bigg|_1^2 - \int_1^2 \frac{e^{u-1}}{u} \, du $$The first and last terms cancel out, leaving us with:
$$ \frac{e^{2-1}}{2} - \frac{e^{1-1}}{1} = \frac{e}{2} - 1 $$Problem 3: Limits to integral
Evaluate the limit:
Solution:
Let \( L = \lim_{n \to \infty} (\frac{n!}{n^n})^{\frac{1}{n}} \)
Therefore, \( \ln(L) = \lim_{n \to \infty} \frac{1}{n} \ln(\frac{n!}{n^n})\)
We know that:
$$ \ln(\frac{n!}{n^n}) = \ln(\frac{n}{n}) + \ln(\frac{n-1}{n}) + \ldots + \ln(\frac{1}{n}) $$Using Riemann Sum (Upper sum):
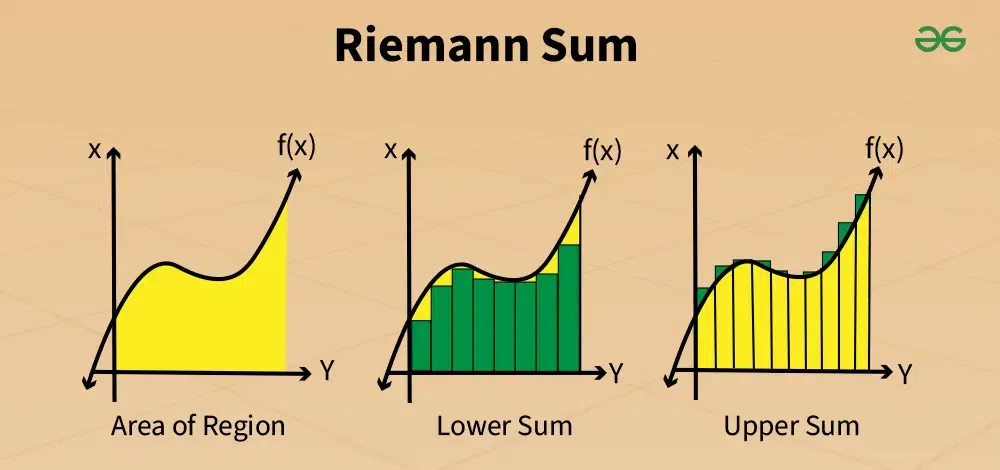
We know that the rectangle width is \(\frac{1}{n}\) and the height is \(\ln(\frac{k}{n})\) for \(k = 1, 2, \ldots, n\). Thus, we can express the sum as:
$$ \ln(\frac{n!}{n^n}) = \ln(\frac{n}{n}) + \ln(\frac{n-1}{n}) + \ldots + \ln(\frac{1}{n}) = \int_0^1 \ln(x) \, dx $$We can now evaluate the limit: